Wikipedia

Resultados de la búsqueda

OCTUBRE :)

1° Clase
Iniciamos conociendo como funcionara el curso de Cálculo Vectorial, el sistema del Blog y de los deberes.

2° Clase
En ésta clase se inicio recordando definiciones de plano (R2) y espacio (R3), para posteriormente iniciar con el tema de Geometría Analítica en R3, con lo que se concluyo que geometricamente una función implícita de 2 variables representa una CURVA en R2 y que la intersección de 2 funciones implícitas genera 1 o más "puntos"; además que geometricamente una función implícita de 3 variables representa una superficie cilíndrica en el R3 y que la intersección de 2 superficies cilíndricas generando "curvas". Además se revisó casos particulares donde la generatriz puede ser para lela a cualquiera de los 3 ejes coordenados.
                                                     
En ésta figura se puede mirar que la generatriz esta paralela al eje Z.

Se culminó la clase mirando un caso de la recta en R3 en donde encontramos la ecuación de la recta, tanto paramétricas, como ecuaciones simétricas.

                                             ecuación vectorial de la recta
ecuación vectorial de la recta en el espacio Ecuación vectorial de la recta.

Ecuaciones para métricas de la recta Ecuaciones parametricas de la recta.

ecuación continua de la recta Ecuaciones simétricas de la recta.


3° Clase
En ésta clase continuamos estudiando a la recta en el espacio y deducimos la fórmula para encontrar la distancia de un punto a la recta.

                                              distancia de un. Una fecha
                                                                distancia de un punto a una recta
También se estudio el ángulo entre dos rectas
                                                dibujo
                                                   ángulo
Alcanzamos a estudiar también el tema del plano en R3 (espacio)




       Otro tema es la ecuación segmentaria del plano

                                               ecuación canónica en el espacio
                            ecuación canónica de la recta en el espacio
             coeficientes
Además de la ecuacion normal del plano:

Ecuación normal del plano

4° Clase
Empezamos con el concepto de factor normalizante (u)
                                                                     
Además encontramos la fórmula de la distancia de un punto al plano.
                                           
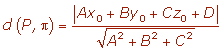
                                                      distancia punto plano
Y estudiamos el producto mixto que sirve para encontrar la ecuación del plano conociendo 3 puntos


Ec. Vectorial del plano dados 3 puntos "Producto Mixto"

Además de comprobarse que mediante el producto mixto se puede conseguir el volumen de un paralelepipedo formado por 3 vectores.

Además de conseguir la fórmula para la recta determinada por la intersección de 2 planos.
                                       


Deducimos la ecuación del Haz de planos

                                                   

5° Clase
La clase comenzó con la definición de la ecuación de la esfera
                                              
Ec. Cartesiana o general de la esfera
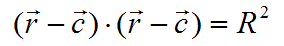
Ec. Vectorial de la esfera

Posteriormente se estudio las superficies de segundo orden, dentro de las cuales interiorizamos cilindros y superficies cuadráticas. Se realizaran superficies con generatriz paralela a los diferentes ejes coordenados.
       
En la parte de evidencias se mostrara el proceso a seguir, para encontrar la forma de la superficie elipsoide.
6° Clase
En ésta clase empezamos realizando ejercicios de graficar la superficie z=cos(y) 
                                    
Además se revisó la muy conocida "Silla de Montar", que es la representación de la Ecuación del Paraboloide Hiperbólico.

                               
Éste día también iniciamos con el tema de las Funciones Vectoriales y Curvas en R3 que definimos:

\vec{F}(t)=(f1(t);f2(t);f3(t))

En este tema profundizamos revisando conceptos de casos particulares (funcion que representa una curva plana en R2) y casos generales (el dominio o el rango de la función es la intersección de los dominios y rangos de cada componente).

Se miro definiciones de límites, continuidad, derivadas e integrales de una función.

7° Clase
Empezando la clase se reviso diferentes ejercicios sobre ecuaciones cartesianas de curvas, como la ecuación de la "Hélice Circular"
z=arctan(y/x)
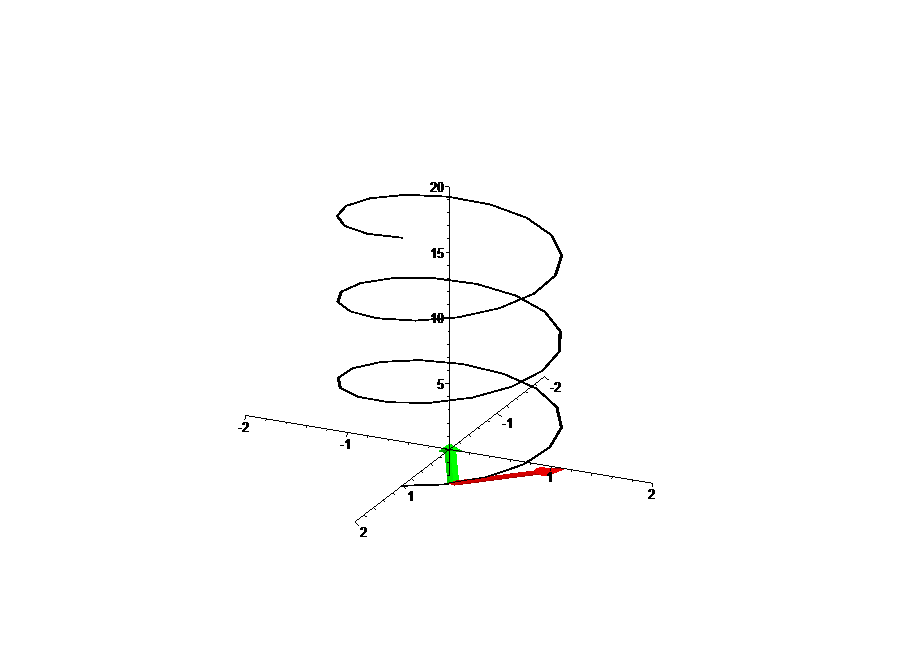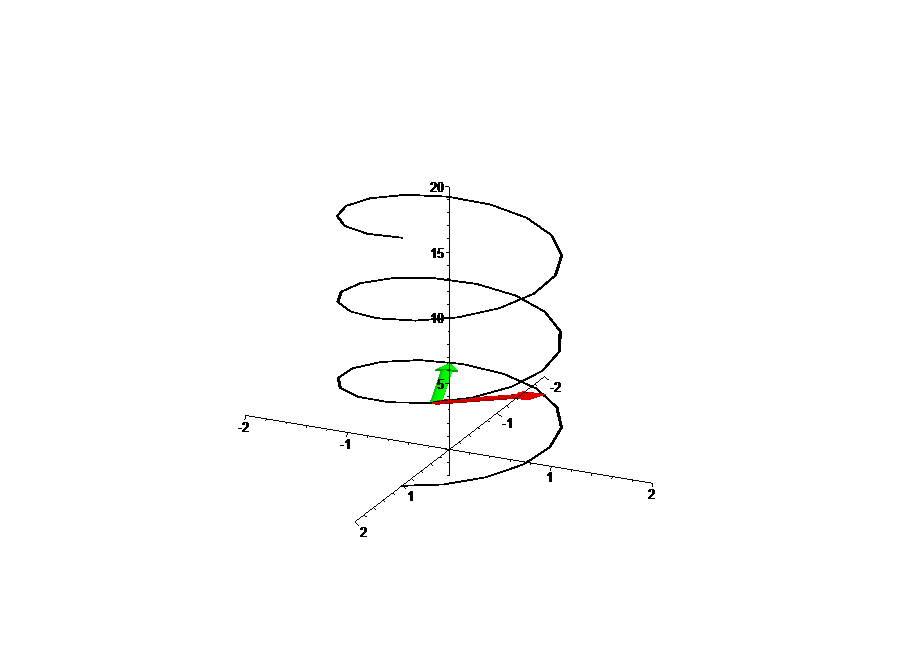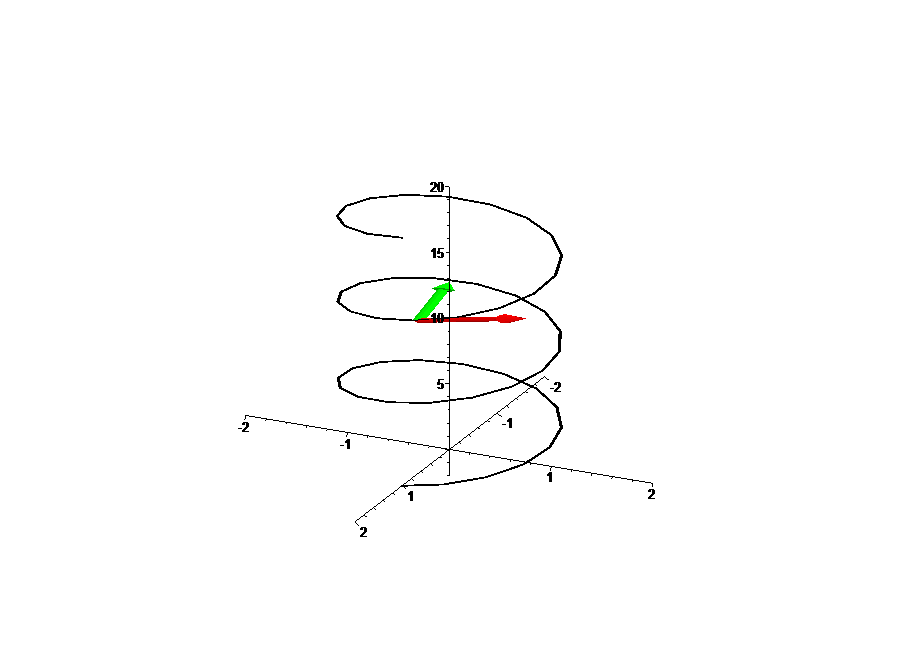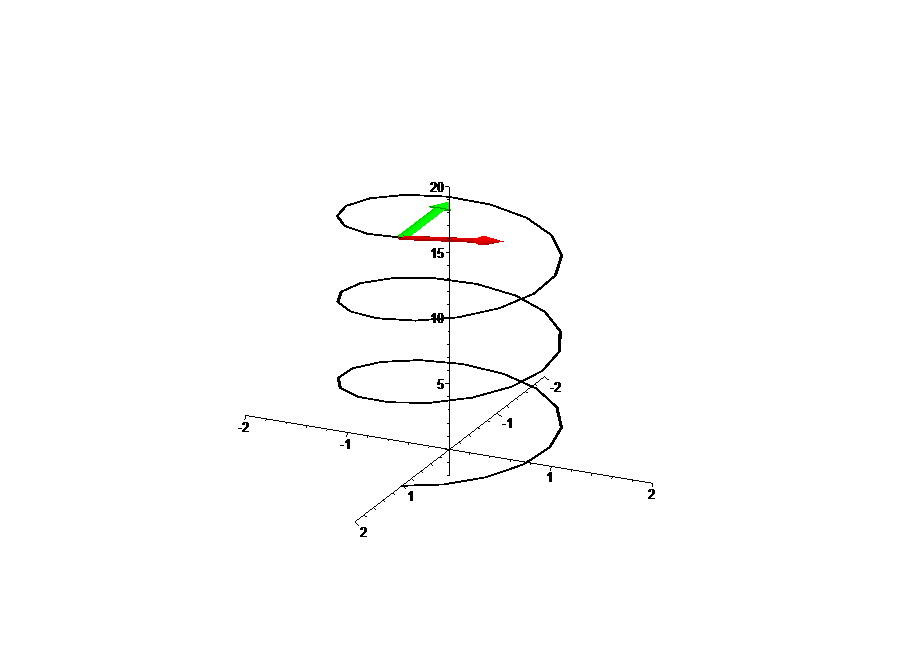
Iniciamos el estudio del Triedro Móvil.
A partir de la primera y segunda derivada de "r" se obtienen diferentes fórmulas:
  Vectores Normal, Tangencial y Binormal

Se dedujo ecuaciones de rectas y planos:

\frac{x-x0}{Tx}=\frac{y-yo}{Ty}=\frac{z-z0}{Tz} Ec. de la Recta Tangente
 \frac{x-x0}{Bx}=\frac{y-yo}{By}=\frac{z-z0}{Bz} Ec. de la Recta Binormal
\frac{x-x0}{Nx}=\frac{y-yo}{Ny}=\frac{z-z0}{Nz} Ec. de la Recta Normal Principal

Bx(x-x0)+By(y-y0)+Bz(z-z0)=0 Ec. Plano Osculador
Nx(x-x0)+Ny(y-y0)+Nz(z-z0)=0 Ec. Plano Rectificante
Tx(x-x0)+Ty(y-y0)+Tz(z-z0)=0 Ec. Plano Normal

Y se culminó con la deducción de las Ecuaciones de Frenet - Serret:

\frac{d\hat{T}}{dt}=k\hat{N} \left\|{\frac{d\vec{r}}{dt}}\right\|
1° Ec. de Frenet - Serret:

\frac{d\hat{B}}{dt}=- \tau\hat{N} \left\|{\frac{d\vec{r}}{dt}}\right\|
1° Ec. de Frenet - Serret:

\frac{d\hat{N}}{dt}=( \tau\hat{B}-k\hat{T}) \left\|{\frac{d\vec{r}}{dt}}\right\|
1° Ec. de Frenet - Serret:

\tau es la curvatura de torsión.
Y finalmente se revisó los Tipos de Curvatura:

1) Curvatura de Flexión: Llamada simplemente curvatura, se entiende por la región de cambio de dirección del vector tangente con respecto a la longitud de arco.

\frac{d\hat{T}}{ds}=K\hat{N}

Pk=\frac{1}{k} , es el Radio de Curvatura

2) Curvatura de Torsión: representa el alejamiento o acercamiento del plano osculador a la curva C, se entiende como la variación del ángulo del vector binormal con respecto a la longitud de arco.

\frac{d\hat{B}}{ds}=- \tau\hat{N} 

P \tau=\frac{1}{ \tau} , Radio de Curvatura de torsión

No hay comentarios:

Publicar un comentario

Suscribirse a: Entradas (Atom)